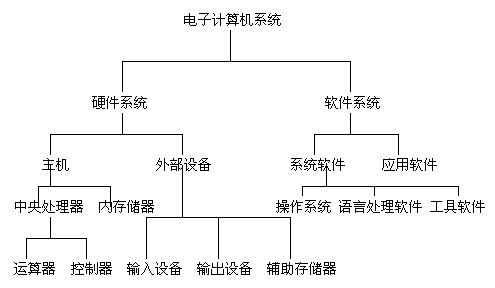
第一章:计算机系统基础知识
1,计算机系统的硬件组成
CPU:Central Processing Unit, CPU
运算器是对数据进行加工处理的部件,它主要完成算术和逻辑运算。
控制器的主要功能则是从主存中取出指令并进行分析,控制计算机的各个部件有条不紊的完成指令的功能。
存储器是记忆设备——1,内部存储器(Main Memory, MM, 简称内存) 2,外存
寄存器是CPU中的记忆设备,用来存放指令,数据及运算结果。
2,计算机的类型和应用领域
按照功能是否单一,计算机可分为通用计算机和专用(嵌入式)计算机。
按照CPU指令系统架构,计算机分为复杂指令系统计算机(Complex Instruction Set Computer, CISC) 和 精简指令系统计算机(Reduced Instruction Set Computer, RISC).
按体系结构及指令处理方式,计算机分为四种(X指令流X数据流,simple,multiple)
3,机器数和码制
带符号的机器数可采用:
1,原码:最高位是符号位,其余的(n-1)位表示数值的绝对值
0有两种表示方式:000000...或10000..(-0)
2,反码:负数的反码是其绝对值按位求反。
0有两种表现方式:00000000或1111111
3,补码:负数的补码等于其反码的末尾+1。
4,移码:移码表示法是在数X上增加一个偏移量来定义的,常用于表示浮点数中的阶码。如果机器字长为n,在偏移2n-1的情况下,只要将补码的符号位取反便可获得相应的移码表示。
0= 100000....
1 = 10000...1
4,定点数和浮点数
定点数就是表示数据时小数点的位置固定不变。纯整数,纯小数。
原码/反码 定点整数范围: -(2n-1-1) ~ +(2n-1-1)
原码/反码 定点小数范围: -(1-2-(n-1)) ~ +(1-2-(n-1))
补码/移码 定点整数范围:-2n-1 ~ +(2n-1-1)
补码/移码 定点小数范围:-1 ~ +(1- 2-(n-1))
浮点数是小数点位置不变的数,能表示更大范围的数
一个含小数点的二进制数N可表示为更一般的形式:
N = 2E * F
其中,E称为阶码,浮点表示法中,通常为带符号的纯整数,
F为尾数,通常为带符号的纯小数。
IEEE754(IEEE制定的浮点数工业标准)中,表示为SPM
其中,S为数的符号位0|1。P为阶码,通常用移码表示,M为尾数,用原码表示,且规格化,去掉首位的1。
值 存储为 指数 偏移量
单精度: 1位符号位(s)、8位指数(e),23位尾数(m,共32位) 127(7FH)
双精度: 1位符号位(s)、11位指数(e),52位尾数(m,共64位) 1023(3FFH)
扩充精度: 1位符号位(s)、15位指数(e),64位尾数(m,共80位) 16383(3FFFH)
阶码用移码表示,移码的偏移值并不是通常n位移码所用的2n-1,而是2n-1-1,这是因为尾数规格化后必须为0.100..0,而我们现在尾数用1.000..00表示,即尾数左移1位,所以阶码偏移值为2n-1-1。
也可以用(指数补码-1),然后符号位取反获得。
5,BCD码
四位二进制来表示一位十进制,二-十进制编码,简称BCD编码。
8421码——普通
余3码——在8421码基础上,把每个数的代码加上0011后构成
格雷码——相邻的两个代码之间只有一位不同。
如果使用BCD码进行计算,可能需要进行修正。
如8421码中,6+7= 0110 + 0111 = 1101,不在BCD码表示范围里。修正的方法是 本位+6,向高位进1。
1101+ 0110 = 0011 为3,高位为1,结果为13.
余3码进行计算中,从最高位产生的进位是真正的进位,对每4位的结果,如果是小于等于9的,则减3,如果大于9,则加3.
6,汉字编码
汉字内码:
GB2312-80 两个字节存放一个汉字的内码,每个字节最高位置为1。可表示2^14个 16384 汉字。
ISO/IEC 10646标准,通用多8位编码字符集 UCS(Universal Code Set):4个八位码。 组(最高位不用),平面、行、字位。
7,校验码
码距是校验码中的一个重要概念,指一个编码系统中任意两个合法编码之间至少有多少个二进制位不同。
(1) 奇偶校验码:在编码中增加一个校验位来使编码中1的个数为奇数或者偶数,从而使码距变为2。只可以检测代码中有奇数位出错的代码。
水平奇偶、垂直奇偶、水平垂直奇偶校验。
(2) 海明码:
一般来说,若信息位为k位,冗余位为r位,则数据位n=k+r,用r的监督关系式来产生r个校正因子,区分无错和在n个不同的位置的一位错,则要求满足公式 2r >= n+1 或 2r >= k+r+1
此式子称为海明公式,r叫海明距离,若k=4时则r>=3,当取r=3时,n=k+r=4+3=7
校验码位置为 2n
8位数为例(不完全,只适合初级理解)
P1 = 0 1 3 4 6
P2 = 0 2 3 5 6
P3 = 1 2 3 7
P4 = 4 5 6 7
(3) 循环冗余校验码:
求CRC编码时,采用的是模2运算。
8,逻辑代数与逻辑运算
常用逻辑公式:
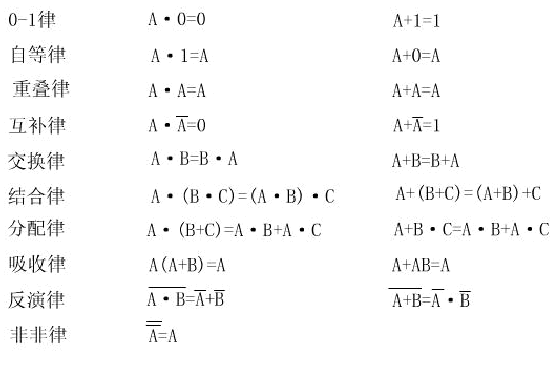
其他公式: 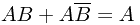
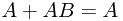
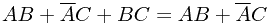
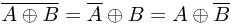
例题:化简逻辑表达式 
9,补码加减法溢出判断机制
1,双符号判决法:
用额外两位表示符号,00表示正号,11表示符号。则溢出时结果的两个符号位就不一样了,从而可以判定发生溢出。 VF= S2 ^ S1
例1: x = +110110, y = -110011
则x - y = x + (-y)补码,即为 00110110 + 11001101
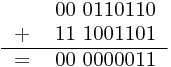 0^0 = 0,没有溢出
0^0 = 0,没有溢出
例2: x = -1111000, y = -10010
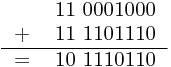 1^0 =1,溢出
1^0 =1,溢出
2,进位判决法:
Cn-1表示最高数值位想最高位的进位,Cn表示符号位的进位, 则 VF = Cn-1 ^ Cn 表示溢出
3,同号数求和或异号数求差时,可根据符号位与进位判定溢出。 VF = SF ^ CF
4, 若用X,Y,Z表示两个操作数及运算结果的符号位。 VF = (X & Y & ~Z) | (~X & ~Y & Z)
10,浮点运算
1,浮点加减
1)对阶,使两个数阶码相同
2) 求尾数和(差)
3) 结果规格化
4) 舍入。尾数最低位因为过长被丢掉。处理方法有 截断法 末位恒1法,0舍1入法。
5) 溢出判别。若阶码溢出,则结果溢出。若阶码下溢(小于最小值),则结果为0。
2,浮点乘除
积的阶码等于两乘数的阶码相加,尾数等于两乘数尾数相乘。
商的阶码等于被除数的阶码减去出书的阶码,尾数等于被除数的尾数除以除数的尾数。
然后规格化并判定溢出。
节选自2003年软考试题
若在系统中有若干个互斥资源R,6个并发进程,每个进程都需要5个资源R,那么使系统不发生死锁的资源R的最少数目为_____ 。
A.30 B.25 C.10 D.5
还有一道,2005年11月的试题,同样类型
系统中有4个单位的存储器资源,被n个进程共享,如果每个进程都要求i个单位的存储器资源,那么当————市,系统不会发生死锁。
A n=2, i=4
B,n=4, i=3
C,n=3, i=2
D,n=3, i=3