各进制之间的转换
星海
posted @ 2011年1月19日 09:53
in 通用知识
, 1323 阅读
一。进制概念
1。 十进制
十进制使用十个数字(0、1、2、3、4、5、6、7、8、9)记数,基数为10,逢十进一。
历史上第一台电子数字计算机ENIAC是一台十进制机器,其数字以十进制表示,并以十进制形式运算。设计十进制机器比设计二进制机器复杂得多。而自然界具有两种稳定状态的组件普遍存在,如开关的开和关,电路的通和断,电压的高和低等,非常适合表示计算机中的数。设计过程简单,可靠性高。因此,现在改为二进制计算机。
二。进制转换
1。二进制与十进制数间的转换
(1)二进制转换为十进制
将每个二进制数按权展开后求和即可。请看例题:
把二进制数 (101.101)2 = 1*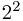 +0*
+0*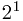 +1*
+1*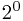 +1*
+1*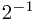 +1*
+1*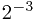 =(5.625)10
=(5.625)10
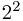 +0*
+0*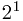 +1*
+1*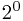 +1*
+1*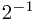 +1*
+1*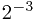 =(5.625)10
=(5.625)10
(2)十进制转换为二进制
一般需要将十进制数的整数部分与小数部分分开处理。
整数部分计算方法:除2取余法
(53)的二进制值为(110101)2
小数部分计算方法:乘2取整法,即每一步将十进制小数部分乘以2,所得积的小数点左边的数字(0或1)作为二进制表示法中的数字,第一次乘法所得的整数部分为最高位。请看例题:
将 (0.95)10 转换成二进制。(0.95)10 =(0.1111....)2
2。 八进制、十六进制与十六进制间的转换
八进制、十六进制与十六进制之间的转换方法与二进制,同十进制之间的转换方法类似。例如:
(73)8 7*8+3= (59)10
(0.56)8 5*8-1+6*8-2=(0.71875)10
(12A)16=1*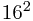 +2*
+2*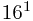 +A*
+A*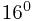 =(298)10
=(298)10
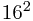 +2*
+2*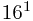 +A*
+A*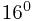 =(298)10
=(298)10
(0.3C8)16=3*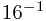 +12*
+12*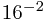 +8*
+8*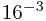 =(0.142578125)10
=(0.142578125)10
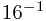 +12*
+12*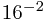 +8*
+8*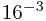 =(0.142578125)10
=(0.142578125)10
十进制整数→→→→→八进制方法:“除8取余”
十进制整数→→→→→十六进制方法:“除16取余” 例如:
(171)10=(253)8
(2653)10=(A5D)16
十进制小数→→→→→八进制小数 方法:“乘8取整”
十进制小数→→→→→十六进制小数方法:“乘16取整”例如:
(0.71875)10= (0.56)8
(0.142578125)10=(0.3C8)16
3.非十进制数之间的转换
(1)二进制数与八进制数之间的转换
转换方法是:以小数点为界,分别向左右每三位二进制数合成一位八进制数,或每一位八进制数展成三位二进制数,不足三位者补0。例如:
(423.45)8= (100 010 011.100 101)2
(1001001.1101)2 =(001 001 001.110 100)2= (111.64)8
2。二进制与十六进制转换
转换方法:以小数点为界,分别向左右每四位二进制合成一位十六进制数,或每一位十六进制数展成四位二进制数,不足四位者补0。例如:
(ABCD.EF)16 = (1010 1011 1100 1101.1110 1111)2
(101101101001011.01101)2= (0101 1011 0100 1011.0110 1000)2 = (5B4B.68)16
 评论 (0)
评论 (0)