google style guide(C++, Python)最新中文版PDF。。
根据项目主页
http://code.google.com/p/zh-google-styleguide/
最新版本于今天凌晨转的。
Google C++ Style Guide:
因个人能力有限,对tex不熟悉,所以这个PDF还有不少瑕疵。主要是:
1,一些地方没有断行,造成无法显示。 不过缺失的行不多,不影响阅读理解。
2,小节索引号重复,应是原始文档的问题,水平有限,暂时无法解决 -__-。。。
HTML格式倒是挺完美-__-,有需要的话可以回帖。有人要的话我再放出来。。
下载地址如下:
http://ubuntuone.com/5Va1HOUaVLi7SYgCC2F4C6
Google Python Style Guide:
最后的表格被撑破了,开头的书目挤在了一起 -____-
http://ubuntuone.com/3ecpLiBbg0gB3OrPl4bhgT
Linux ManPage各章节说明
/* * Section 1 of the manual describes user commands and tools * Section 2 of the manual describes the Linux system calls * Section 3 of the manual describes all library functions excluding the library functions (system call wrappers) described in section 2, which implement system calls. * Section 4 of the manual describes special files (devices) * Section 5 of the manual describes various file formats and protocols, and the corresponding C structures, if any. * Section 6 of the manual describes all the games and funny little programs available on the system. * Section 7 of the manual provides overviews on various topics, and describes conventions and protocols, character set standards, the standard file system layout, and miscellaneous other things. * Section 8 of the manual describes commands which either can be or are only used by the superuser, like system-administration commands, daemons, and hardwarerelated commands. */
Tex初学笔记
\documentclass[12pt,a4paper,twoside,fleqn,leqno]{article}
\usepackage{zhfontcfg}
\usepackage{verbatim}
% fleqn 设置行间公式为左对齐,不是居中
% leqno 设置行间公式的编号为左对齐
% exscale 提供了按比例伸缩的数学扩展库
\author{hoho.sd44}
\title{Tex学习}
\maketitle
\usepackage[top=1in,bottom=1in,left=1in,right=1in]{geometry}
\begin{document}
hahaha\\*
后面是斜线啊,有没有 \textsl{ai} ni \\*
\\测试百分号\% % hahah,你看不到我
\\*你能看到我吗
\begin{comment}
这是一个很严肃的注释哦
\end{comment}
\\上面说了些什么呢?我忘了
\\\
\hyphenation{-} tex-text-texttttxxxxxxxxxxxxxxxxxxxxxxxa
asdfaaaaaaaaaaaaaaaaaaaaaa asdf\\* a % hyphenation在断词时使用{}里的语句,且仅在此时断词 命令\-在单词中插入i个自主的断词点,允许唯一出现的唯一断词点。
asdfaskfalksfjalsflasdflasldf asfdasdfasfdas asdfasdfasdfasdf sdfa asdf\mbox{333 233 2223 33 333 3333 333 } %\mbox使括号中的语句显示在同一行
asdfaskfalksfjalsflasdflasldf asfdasdfasfdas asdfasdfasdfasdf sdfa asdf\fbox{333 233 2223 33 333 3333 333 }\\*
“测试引号'haha'太爽了”\\
网址 http://sexinsex.com/~{}test\\
测试省略号..... \ldots
Footnotes\footnote{This is
a footnote.} are often used
by people using \LaTeX.\
\textit{You can also
\emph{emphasize} text if
it is set in italics,}
\textsf{in a
\emph{sans-serif} font,}
\texttt{or in
\emph{typewriter} style.}\\
\begin{flushleft}
This text is\\ left-aligned.
\LaTeX{} is not trying to make
each line the same length.
\end{flushleft}
%begin{quote}引用,end{quote}结束。
Add $a$ squared and $b$ squared
to get $c$ squared. Or, using
a more mathematical approach:
\begin{displaymath}
c^{2}=a^{2}+b^{2}
\end{displaymath}
or you can type less with:
\[a+b=c\]
%下面这行有错误,不知在那里
\begin{equation} \label{eq:eps}
\epsilon > 0
\end{equation}
From (\ref{eq:eps}), we gather
\ldots{}From \eqref{eq:eps} we
do the same.\\
行间样式和显示样式区别\\*
$\lim_{n \to \infty}
\sum_{k=1}^n \frac{1}{k^2}
= \frac{\pi^2}{6}$
\begin{displaymath}
\lim_{n \to \infty}
\sum_{k=1}^n \frac{1}{k^2}
= \frac{\pi^2}{6}
\end{displaymath}
每一个字母都会被认为是一个变量名,且会相应被排版为此种样式。如果
你想要在公式中排版普通的文本(直立字体和普通字距)
,那么你必须要把这些文本放在$\backslash$textrm\{...\} 命令中(参阅第45 页的第3.7 节)
\end{document}
第一份TEX文件(计算机算法设计与分析(C语言描述)笔记,持续更新)
http://sd44.is-programmer.com/user_files/sd44/File/2.tex
生成的PDF
http://sd44.is-programmer.com/user_files/sd44/File/2.pdf
求职简历:
http://sd44.is-programmer.com/user_files/sd44/File/jianli.pdf
http://sd44.is-programmer.com/user_files/sd44/File/jianli2.pdf
各进制之间的转换
一。进制概念
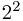 +0*
+0*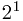 +1*
+1*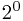 +1*
+1*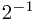 +1*
+1*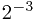 =(5.625)10
=(5.625)10 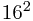 +2*
+2*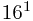 +A*
+A*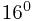 =(298)10
=(298)10 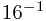 +12*
+12*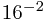 +8*
+8*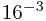 =(0.142578125)10
=(0.142578125)10